ENTREZ À L’ECOLE DU NOMBRE D’OR. SUIVEZ CE PROJET et ECHANGEZ : cdl.dirpt@gmail.com
Historique du projet :
Un pompier breton a contacté le CDL pour finaliser un projet de bergerie à construire selon les règles Phi.
Le projet vise a réduire des dépenses d’entretien d’un grand terrain, puisque 4uatre brebis à l’année sont plus économiques qu’un contrat d’entretien avec une entreprise. Notre professionnel du feu prend soin des dépenses publiques mais aussi des futures brebis qui vont ainsi bénéficier d’un habitat harmonieux original.
Nous avons décidé de l’accompagner….à la recherche de la Toison d’Or
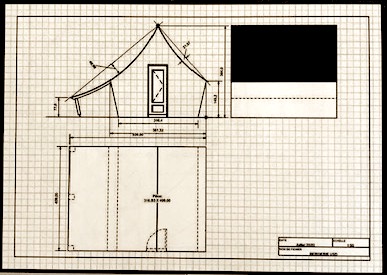
Voici le schéma initial du concepteur. L’idée, le germe.
Ce premier dessin de la bergerie est imaginé autour d’une porte standard du commerce, mais les proportions Phi de ce plan sont encore à mettre en place. Les mesures indiquées sont approximatives, ne pas en tenir compte.
Problématique : Tout en respectant au plus près le design, il s’agit à présent d’inclure le nombre d’or dans ce concept, directement ou en substratum. Un projet pastoral comme celui-ci va s’inscrire dans la vie de la nature, or la nature est directement structurée par le nombre d’or. Qu’il s’agisse d’une bergerie ou du Parthénon d’Athènes, les règles sont les mêmes.
A la fin, quand les proportions seront arrêtées, nous choisirons une mesure pour métrer les esquisses.
Géométrie du projet
Armé d’un logiciel fournissant une règle proportionnée au nombre d’or, notre Ami Patrick.M est parti d’instinct sur un carré comme base d’abri nocturne, en utilisant le quine fourni pour agrandir sa création.
La Bergerie a donc une forme carrée, symbole du monde physique cher à Pythagore, prolongée par un préau, soit au total une emprise au sol de proportion 1 x 1,618. Nous sommes donc partis d’un carré pour construire ( au compas il va de soit) un rectangle d’or.
Patrick utilise donc la loi de réversibilité, privilégiant le carré, lieu où les animaux passeront leurs nuits.
Loi de réversibilité
« Tout carré peut être construit avec des rectangles d’or et inversement.«
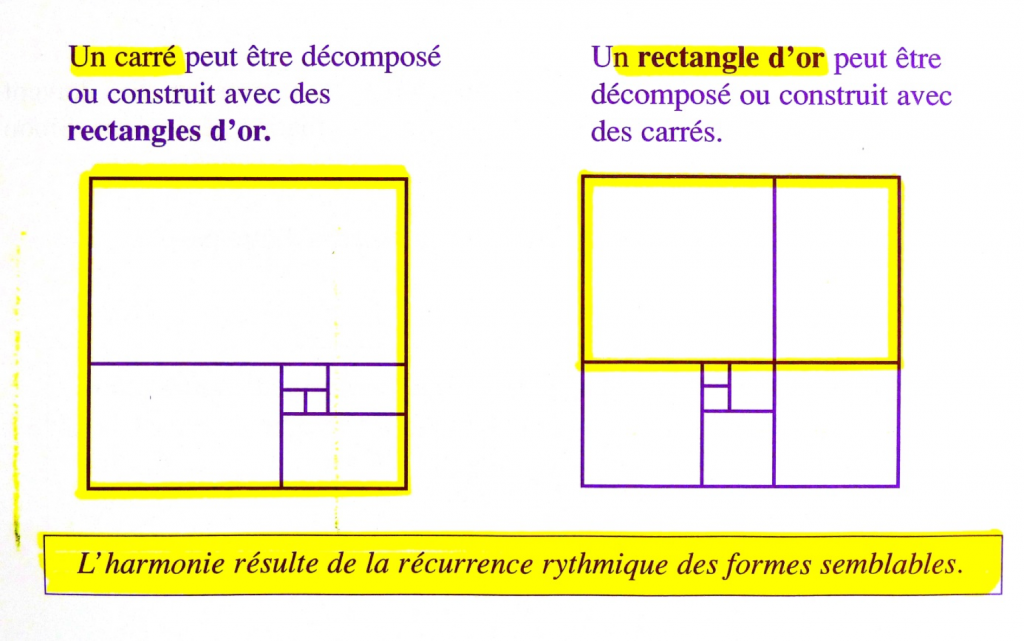
Après modification, il livre ainsi, l’esquisse suivante :
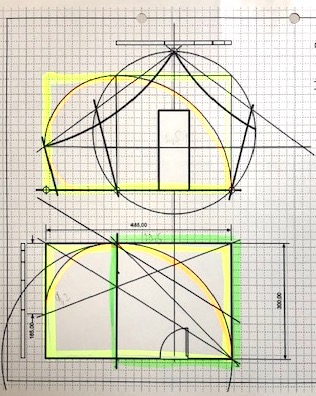
Remarquons :
- en haut de la feuille, la règle proportionnée ou Quine
- en vert, en bas sur le plan, le carré générateur.
- en jaune, toujours sur le dessin du bas, le préau prolonge le carré, créant un rectangle d’or.
- en élévation, vue de face, soit le dessin du haut, nous retrouvons le carré générateur qui contient la porte d’entrée.
- le toit s’abaisse en arc de cercle jusqu’aux limites du rectangle Phi.
- A nouveau, ne pas tenir compte des mesures indiquées.
- En orange, une spirale de croissance apparaît
A propos de la forme Carrée
Au regard de la Tradition, le carré est « la première pierre » d’un édifice, d’une intention, d’une création.
Il est aussi la base du système GGS, canevas ou grille à module carré qui permet de relier et de retrouver les proportions des monuments anciens, leur orientation, leurs liens avec nos luminaires, la Lune ou le Soleil.
Le carré permet une décomposition gnomonique par croissance ou décroissance continue jusqu’à l’apparition de la spirale logarithmique (Ghyka). Dédoublé, il donne le double carré générateur du nombre d’Or, soit l’octave.
Le carré, générateur de forme et pierre angulaire, appartient aussi bien à la série statique que dynamique selon Hambidge.
La démarche de notre ami Patrick s’inspire donc d’une vieille Tradition, qui partait d’une forme statique, c’est-à-dire d’une forme utilisant des nombres entiers ou fractionnaires, pour évoluer vers une forme dont les nombres sont incommensurables.
Le carré est l’une des figures-mères des sciences anciennes. Son nombre est 4, puisqu’il a 4 côtés.
Les nombres fondamentaux, nombres-souche, font partie des 22 nombres figuratifs qui relèvent du système des 22 polygones réguliers inscriptibles dans le cercle.

3 mères, 7 doubles, 12 simples
Parmi les trois nombres fondamentaux, 4 est le multiplicateur, 3 et 5 sont des multiplicandes ( trois pour le triangle, 5 pour le pentagone)
Les formes-figures du 3 et du 5 peuvent se considérer comme issues du 4.
Ceci est très important, car on considère que le 4 est une figure générique. D’ailleurs, le 5 ou pentagone, procède du carré et du triangle, via le nombre d’or.
Dans un autre système de construction, dont les modules carrés forment des grilles ( le système GGS), nous avons la confirmation de cette paternité.
Le 4 est le module de base, le module de croissance par excellence. C’est lui que nous retrouvons dans tous les temples, que ce soit à Balbek, dans les pyramides égyptiennes de Giseh, à Ur, à Göbekli Tepe, dans l’implantation des mégalithes etc.
Et nous disons module de croissance volontairement, faisant ainsi le lien avec le nombre d’Or qui est le coefficient de croissance le plus courant du monde vivant .
Aujourd’hui, c’est par le carré que nous pouvons analyser les sites les plus anciens et découvrir qu’ils sont le fait d’une école géométrique commune sur la planète.
Le 4 ou carré, a donc un rôle fondateur dans la réalisation d’une idée, idée qui pourra se développer dans pratiquement toutes les formes, par la croissance ou la multiplication du carré-module-initial.
Exemple entre tous, le double carré, soit deux carrés accolés, ou rectangle de 2 sur 1, génère le nombre d’or ( par sa diagonale).
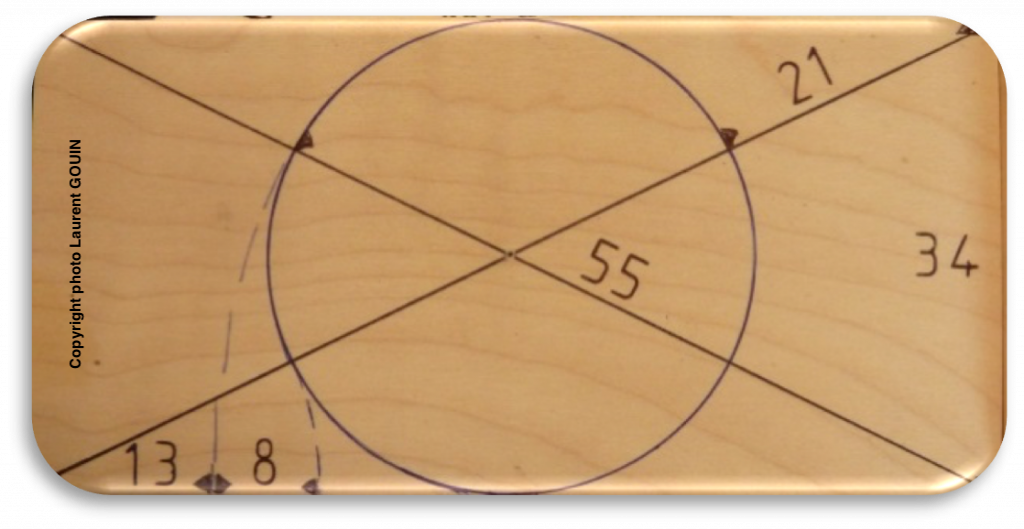
Le carré et la géométrie-grille GGS construisent aussi des spirales, formes dynamiques. Nous sommes vraiment là sur des fondamentaux.
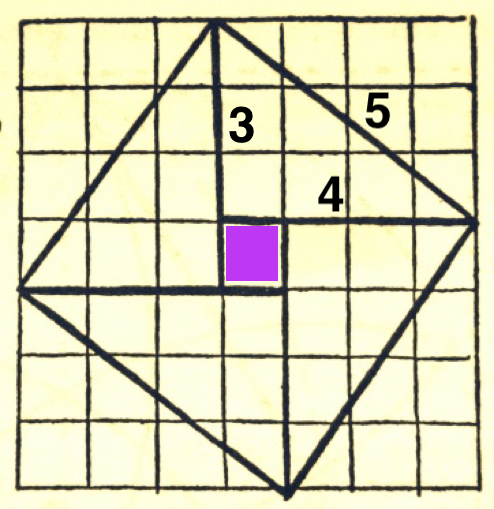
La surface carrée, figure-souche de la Tradition, distribue des spirales mais aussi le triangle 3-4-5 appelé par la plupart des auteurs « triangle sacré égyptien » ou encore triangle de Pythagore. C’est le triangle rectangle dont les côtés sont proportionnels aux nombres 3-4-5 , le seul triangle qui forme un série arithmétique.
Fin provisoire,
La suite bientôt ……avec les nouveaux plans.